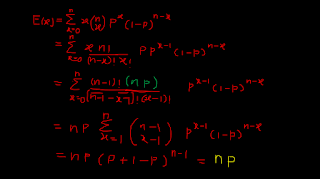Binomial distribution?

 I was busy a little bit with few of my freelancing projects last three days. really sorry for the late answering. Anyway I could see in my website someone has asked to show above expression equals to 'np'. really that's pretty easy to do with the expansion. then you should know the variable here. that's just 'x'. 'x' has been varied from 0 to n. then you guys can keep expanding combinations as shown as above. that's quit different for A/L guys. But you may be taught this exactly once you go ahead furthermore. This is related to a basic stagedy in universe. It doesn't make sense yet but keep this too in your mind thoroughly. Every thing were in old syllabus before 2000. somehow once you recognize that n and p are constants you should be able to take them out. remaining part, you may confused sometimes coz I haven't shown that step there. summation can be separated into two parts as x=0 + form 1 to n. then you may see that x=0 will be dropped simply. so what a familiar expression is this now. are you astonished with it. it was caught simply? yeah that's the binomial expansion of (p+1-p)^n-1. whatever n is, whole part is gonna be equal to 1. that's the law of mother nature, one day you may realize it.

And also I have a kind request for math lovers, please try to understand the reality of integration. https://youtu.be/LMJaZJ69WkI

Integration

Don't forget to share your ideas.

By:SAPUMAL SENADEERAGE SASANKA SAGARA    

Forces along a single plain(Q4)

Today i use to explain it in english coz of some inconvenience with sinhala fonts,anyway i determined  considering this question most of the student had some issues to understand the term 'formed line' it was nothing else when we form a cylinder with a rectangle theres a connection line we use to paste two edges together .so along this form lines A and B cylinders with given measurements then another C cylinder also was given .AB are on C where A touches horizontal  floor.as explained figure was sketched out fairly. All students need to know that you wanna avoid from sketching out special cases. Always try to pay attention on all data you are give then sketch out them with slants fairly .others can be predicted with your knowledge of geometry or calculations based on plane trigonometry .the line which connects A and B is not horizontal .if it doesnt make sense please pay attention on basic trigonometric calculations with projections. Its better to consider M around A considering compound body AB .thats a separated body no more .even theres no reactions between AB so far.If you have any doubt so far please be kind enough to put them here.other questions also may be solved as soon as possible .thank you

Power of Royalists

 

ඉහත රාජකියන්ගේ මෑත කාලයෙහි ප්‍රශ්න පත්‍රයෙහි වන ඝර්ෂණය සහිත ගැටුම් ගන්නට රුකුලක් වනු නියා ඉහත ආනත තලයක උදග්රයෙහි වන mg බර ඝන ගෝලය ගෙන ගණනයකින් පෙන්වා ඇත්තේ බ්‍රමණ චාලක ශක්තිය ඝර්ෂණය නිසා උත්පාදනය වුවකි මෙය කිසිකලෙක කවුරුන් ඉස්සරවිද යන්න කිවනොහැක ,ලෝකයෙහි මෙවන් සමකල්ය වූ සමගාමී සිදුවීම් පවතී (අභිධර්මහිද මෙවන් ධර්මතා විස්තර කෙරේ සමාන්තර බිත්ති දෙකක් මද සිට එක බිත්තියකින් අනෙකට ලංවූ කල කුමකින් මුලින් දුරස් විද කුමකට මුලින් ලන්විද ලෙස වෙන්ව කිව නොහැකිසේ නොවේද ) ලිස්සිමෙන් තොර බ්‍රමණය සලකන්න ගෝල අක්ෂය සමුද්දේශ රාමුවේ සහ පෘථිවි සමුද්දේශ රාමුවෙහි චලිතය ගැන සිතන්න .බොහෝ දරුවන් ආරම්භයේ වූ ගුරුත්වාකර්ෂණ විභව ශක්තිය උත්තාරණ චාලක ශක්තිය සහ බ්‍රමණ චාලක ශක්තිය පමණක් නොව ගර්ශනය නියාවෙන් හානිවූ ශක්තියටද සමකිරීමට වෙරදරයි .මෙහිදී ඔබ අවබෝධකරගැනීමට වෙර දැරිය යුත්තේ ඝර්ෂණය නිසා හානි වන ශක්තිය බ්‍රමණ චාලක ශක්තියට සර්වසම වන බව මිසක එය ඇතිවීම කිනම් කලක සිදුවීද යන්න නොවේ සැබවින්ම එය සමගාමිව සිදුවූ දෙයකි.ගණනය කිරීම ඉහත පෙන්අවා ඇත.රාජකීය ගන්නද නුවනින් සිතා විසඳීම යෙහෙකි ,අප මේ  සියලු සාකච්චා කර ඇත්තේ නිව්ටෝනියානු යාන්ත්‍ර විද්‍යාව සමග බවද සිහි තබා ගන්න .ඉන් එහා ක්වොන්ටම් යාන්ත්‍ර විද්‍යාවද පරයා සිතන්න අධිතන් කරගන්න .ඉහත ගැටලුව විසඳිය හැකි තවත් ක්‍රමයක් යෝජනා කරන්න . නිව්ටන්ගේ පරික්ෂණාත්මක නියමයෙහි ඔහු කල නිවැරදි ඉදිරිපත් කිරීමද නුදුරු දිනක පෙළගැස්වීමට බලාපොරොත්තු වෙමි .මිට අමතර අප සිසුන් කිහිඅදෙනෙක් එවූ ගැටළුද ඉඩක් ලද විගස සාකච්චාකරනු ඇති . 

Be aware from special cases

 තවත් අප දරුවෙකුග්ර් පැනයක් වුයේ පෙර බ්ලොග් පිටුවෙහිම අන්තර්ගත 97 ගැටලුවයි .

මෙහිදී බොහෝ දරුවන් බලරුපසටහන ගොදනගිමෙහි ලා හෙම්බත්වන කරුණු කිහිපයකි.බොහොදරුවනට බෝම්බසයෙහි ජ්‍යාමිතිය ගැනද කිසිදු අවබෝදයක් නැති සැටියි .සමාන්තරාස්රහිම විශේශිට වූ පාද හතර එකිනෙකට සමානව විකර්ණ එකිනෙකට ලම්භකව සමච්චේදනය වන මුත් එය සමචතුරස්රයක මෙන් එකිනෙකට සමාන නොවෙයි .ඊසමගාමිව සිදුවන තවත් ජ්‍යාමිතික ලක්ෂණ නම් විකර්ණා මගින් කොන සමචේදනය වීමයි මෙය නොදනී නම් බල රුපසට හඬෙහි කොන ලකුනුකිරිම සිහිනයක්ම වනු ඇත .AC විකරණය යටි අත සිරස සමග තිඉට කෝණයක් සාදන බව විශේෂයෙන් කියා ඇත .ආස්තරය ඒකාකාර බැවින් විකර්ණ චේදනය වන ලක්ෂය ඔස්සේ සිරස්ව පහලට ක්රියාරෙකාව වන බව දත යුතුය .එසියල්ල අවබෝදකරගත් කල බොහොයවලුන්ට පවසා ඇති පරිදි එකිනෙකට b දුරකින් එකමතිරස් මට්ටමක වූ සුමට නැති දෙක මත රෝම්බසය නැංවීම අපහසු සැටියි .බොහෝ දෙනා අභිලම්භ ප්‍රතික්‍රියා දෙකඩ රෝම්බස්යෙහි කේන්ද්‍රය ඔස්සේ යායුතුයි සිතයි. ඒකතල බල තුනක් යටතෙහි ආස්තරය සමතුලිතවන බැවින් අවශ්‍යතාවය අභිලම්භ ප්‍රතික්‍රියා හටගැනීමට වූ නිතිය අනුගමනය කරමින් බලතුන ඊක ලක්ෂවිමයි .ඉහත ආකාරයට ලාමිගේ ප්‍රමේය දීමෙන් අභිලම්භ ප්‍රතික්‍රියා දෙකඩ A ලක්ෂය වටා රෝම්බසයෙහි සමතුලිතතාවය සැලකීමෙන් ඝුර්ණ ගැනීමෙන් a සම්බන්ධකල හැක තවද ලම්භක දුර ඉහත දක්වා ඇති ත්‍රිකෝණය මගින් b ට සම්බන්ධකරමින් පහසුවෙන් ප්‍රකාශනය සාධනය කල හැක .මෙහි අවසන් අවශ්‍යතාවය ලබාගැනීමේදී ඔබ දැන් පවතින සාධාරණ අවස්තාව වෙනස්වියහැකි ආකාරය ගැන මෙනෙහි කල යුතුය .ඉතින් මෙයම භාවනාවක්ම නොවේද .ඒසී දකින කල නනාදැති  නොවෙනස් විය යුතුය බර ක්‍රියා රේඛාව නිතැතින් සිරස්ව පවතී,(මේ පිලි බැඳ වෙනම ලිපියකා උදාහරණ සහිත ප්‍රක්ෂිප්ත සහ ගුරුත්ව කේන්ද්‍ර ගැටළු සහිතව පෘථිවි වක්රතාවයද සලකා විස්තර කිරීමට බලාපොරොත්තු වෙමි අපදන්නා වෘත්ත පාද වලට අතිරේක තරමක් සංකීර්ණ බහුවලික හා ගෝලීය ත්‍රිකෝණමිති පවතී අප තවම විෂය නිර්දේශය තුල අධ්‍යනය කරනුයී තලයක් තුල පමණි )එවිට AC අක්ෂය යටි සිරස සමග කෝණය ශුයයේ සිට 90 -ඇල්ෆා අතර විචලනය විය හැකි නොවේද .දැන් අසමානතාවය ගොඩනගා කෝසයින තිටා ඉවත් කරන්න .බොහොමයක් දරුවන අවසන් පෙන්වීමට ඇති ප්‍රතිඵලය හොඳින් නිරීක්ෂණය නොකරයි .මනික්ගලට පයින් ගසන කනයා බඳුය .අතිශය අවාසනාවකි.පිළිතුර දී ඇත .කලයුතු වන්නේ එයට යායුතු නිවැරදි මාර්ගය සැකසීම පමණි. ඉතින් අවසාන අසමානතාවයෙහි තිඉට නැත එඔස්සේ තිඉටා ඉවත්වීමට තිට මත පදනම් වූ අවශ්‍යතාවයක් ගැන සිතන්න .

(බොහෝදෙනා බලත්රිකොන ප්‍රමේය සහ සයින ප්‍රමේය පටලවාගේනතයි සිතේ මෙය වෙනයම් ක්‍රමයකින්ද ලබාගැනීමට උත්සාහ කරන්න ,ලාමිගේ ප්‍රමේය ලැබෙනුයේ බල ත්‍රිකෝණ ප්‍රමේය සහ සයින ප්‍රමේයයෙහි සුසංයෝගයකිනි ලාමිගේ ප්‍රමේය සත්‍ය වුද විලෝමය සත්‍ය නොවේ ,ඉදිරි දිගුවක මේ සියල්ල එකින් එක ඉඩක් ඇති පරිදි දිග හරිමි )

Light post

 මෙහි එන 96 පැනයද මගෙන් සිසුවෙකු ඇසු එක ප්‍රශ්නයකි .බොහොඕ දරුවන් මෙහිද බල රුඋපසටහන නිවැරදි ආකාරව ඇඳීමට නොහැකිව අසරණවූ බවක් හැඟෙ අ.මෙහි සිරස් කණුවක් සිරස් තලයක සමතුලිතතාවය පිලිබඳ සාකච්චාකෙරී .මෙහිදී බොහෝ දෙනා අසු ප්‍රශ්නය නම් කණුවේ උසෙහි ඇති සම්බන්දතාවයයි .මෙහි කණුවේ උසක් අවශ්යනත මන්ද කණුවේ යට සිට a හා b උසින් තන්තු ආඳා කනුව මත සිරස් ප්‍රතික්‍රියාව බර මෙන් දෙගුණයක් වීමට සකස්කර ප්‍රමාණවත් දත්ත සපයා ඇතිබැවින් හා කනුව සිරස්ව සමතුලිතව ඇති බැවිනි .බොහොඕ දරුවන් නානාවිද සමීකරණ තිරස් සිරස් බල සමතුලිතතාවය ඝුර්ණ මුලධර්ම භාවිතයෙන් විශාල සමීකරණ ප්‍රමාණයක් හුදු අරමුණකින් තොරව ලබා ගැනීමටත් එතුල පටලිවිලි වලට නිරතුරුව බන්දුන්විමත් සුලබව සිදුවීමකි.එමනිසා කෙසේ හෝ සැදීම නොව නිසි අරමුණකින් අවසන් පිළිතුර කරා මෙහෙයවිමම යෙහෙකි . පළමුව ඔබ කනුව මත ඇතිවන ප්‍රතික්‍රියාවේ සිරසට දරන ආනතිය තිඉටා ගණනය කල යුතුවෙයි .කණුවට පමණක් බලපවත්වන බල පළමුව තේරුම්ගන්න .තන්තු දෙක මගින් කනුව මත යෙදෙන ආතති බල කනුවී බර හා කනුව ස්පර්ශලක්ෂයෙහි ප්‍රතික්‍රියාව නම් ඒවා බව දතයුතුය. දැන් බොහෝ සිසුන් ඉහතකිආකාරයට tan තිටා සෙවීම අරඹයා සිරස් තිරස් සමතුලිතතා යොදමින් T 1  , T2 හා R සෙවීමට වෙහෙසේ නමුත් පළමු සමීකරණය දෙස හොඳින් බලන්න R සෙවීම අත්‍යාවශ්‍ය නොවේ කණුවේ සමතුලිතතාවය සලකමින් R sin තිඉටා ට ලබාගත් සම්බන්ධතාවය බලන්න  T 1  , T2 වලින් ඔබට ලැබෙනු ඇත ඉතින් A හා B දෙකෙළවරින් කණුවේ සමතුලිතතාවය සලකමින් ඝුර්ණ ගතහොත් එය පහසුවෙන්ම සෙවිය හැක .බිය නොවන්න සිරස් සමතුලිතතා සලකමින් වෙහෙස වී සෙවූ කලද මෙයම පැමිණෙනු ඇත මදක් සුළු කෙලියී නිරතවියයුතුය කාලය පියඹා යාම ඔබට සිදුවන අවාසියෙකි දැන් 1 හා 4 භාවිතයෙන් ගතනොහකිවීද ?(ත්රිමානයේ සමතුලිතතාවය විෂය නිර්දේශය තුල නොමැති නිසා සුළගින් හෝ අව්වෙන් සිදුවන බාදා කාරී නැත)

 

මෙහිලා බල රුපසටහන නිවැරදිව අන්දගැනීම බොහොඕ දරුවනට මුහුණ පෑමට සිදුවූ පොදු කරුණකි. නමුදු දරුවනි ඔබ පළමුව ගැටලුව හොඳින් කියැවීම යෙහෙකි. කුහර ගෝලයකින් තනු අරය a වූ පාත්‍රය පිහිටවූ ආකාරය විස්තර කල තිබේ එය වටහාගැනීමට නොහැකිව දරුවන් එය පැටලුනු නූල් පන්දුවක් බවට පත්කරගෙන තිබුණි. පළමුව මෙහි ගැට්ටේ එක එක ලක්ෂයට අඳි අරය යනු පාත්‍රයෙහි අක්ෂයට ලම්භකව ගැටිය හරහා යන තලය අදහසවේ(සැකෙවින් ගත කල ගැටියේ තලය නොවේද ) ඉතින් මෙය සිරසට සාදන කෝණය ඇල්ෆා ලෙස දී ඇත .බොහෝ දරුවන්ට මෙම කෝණයේ මනිනලද ඇත උඩු සිරසද යටිසිරසාද වශයෙන් ගැටලුකාරී තත්ත්ව තිබෙනු දැක ඇත.මෙහිදී මෙවන් ගැටලුවක දෙනලද කෝණය නිතතිව සුළු කෝණයකි .එමනිසා එලෙස ලකුණු කිරීමට වගබලාගතයුතුය.A ලක්ෂය ඔස්සේ පවතින අරයද සිරසට බීට කෝණයක් ආනතව පවතින බව දී ඇතිමුත් A හි සාපේක්ෂ පිහිටුම ගැන ඒකතල බලසමතුලිතතාවය සම්බන්ධයෙන් වන ප්‍රමේයයන් හා සැසඳීම යෙහෙකි .A ලක්ෂය පාත්‍රයේ ගුරුත්ගැව කේන්ටිද්යේ‍රයෙහි තලයේ  පහල කෙලවර ගැටියේ තිරස්මට්ටමට ඉහලින් වූවානම් බලසමතුලිතතා නියම කිසවක් පිලි නොපදි (වෙනම බ්ලොග් පිටුවකින් ඒකතල බල පද්ධති හා එහි ජ්‍යාමිතිය අතර සම්බන්ධතාවය ගොඩනැගෙන අයුරු ක්රමානුරුපිව පෙළගැස්වීමට බලාපොරොත්තුවෙමි ).තවද A ගෝලයෙහි කේන්ද්‍රය හරහායන්නා වූ සිරස් රේඛාව පසු කරමින් පහල ගතියට ආසන්න ලක්ෂයක වුද බලසමතුලිතතා නියම පිළිනොපදි.බොහො ගණන් සමග ඔබ ප්‍රායෝගික පැතිකඩද මනාව හසුරමින් පරිනතවන කල මෙවැනි නොව මිට සංකීරණ රුඋපය වුද එකවර ගොඩනැගීමට අවශ්‍ය බුද්ධිය ගොඩනැගේ .ඒවෙනුවෙන් බොහොමයක් ගණන් තමන් විසින්ම විසඳීම යෙහෙකි .අභිලම්භ ප්‍රතික්‍රියා හ්හටගන්නා නීතියට අනුව ස්පර්ශ ලක්ෂ්යේදී පෘෂ්ටයට ලම්භක වන පරිදි A හිදී ප්රුෂ්ටය පාත්‍රය වේ .මෙලෙස හරස්කඩ පරාවල හෝ වෙනයම් හැඩයක් ඔබට ලැබුනානම් අභිලම්භ ප්‍රත්ක්රියාව කවර ආකාරයකට විඉජ සහ ජ්‍යාමිතිකව ගොඩනැගිය හැකිදැයි ඔබම තර්ක කරන්න (විෂය නිර්දේශයට අයත් නොවේ)නමුත් දන්දෙහි බැඳ ගැටියේ වැදුණු කල බොහෝ දරුවන් පුරුද්දට මෙන් දණ්ඩට ලම්භකව ප්‍රතික්‍රියාව ලකුණු කලද ඒ ගැන නිසි අවබෝධයක් නැත.අතිශය සියුම්ව සිතුවහොත් සාපේක්ෂව එම ස්ථානයෙහි පෘෂ්ඨය දන්දවේ.A හි අභිලම්භ ප්‍රතික්‍රියාව විෂ්කම්භය ඔස්සේ හා එය පරිධිය හමුවන ලක්ෂයේම  අනෙක් අභිලම්භ ප්‍රතික්‍රියාව හමුවිය යුතුය .වෘත්තයක ජ්යාමිතියට අනුව එය තහවුරු කරගත හැක .D ලෙස දී ඇති ලක්ෂය දන්දෙ බර රේඛාව පරිධියත් A ඔස්සේ යන තිරස් රේඛාවේ චෙධනයත් වේ කොන නිවැරදිව සොයා ගනිමින් AD ආකාර දෙකකින් සමීකරණ ගොඩනැගීම අතිශය පහසු කරුණකි.එවිට යමෙකුට බලසමතුලිතතා නියම යෝදාඔගත්තේද යයි කුකුසක් ඇතිවිය හැක .අප බලරුපසටහන නිවැරදිව අන්දිමම බල සමතුලිතතා නියම භාවිතා කිරීමකි       

 

මේ බ්ලොග් එක මුලින්ම සිංහලෙන් ලියන්න අවශ්‍යයි කියල හිතුන නමුත් මේහිදී සිදුකරන සියලුම සාකච්චා දැනට අපසමග ඉංග්‍රීසි මාධ්‍යයෙන් ඉගෙනුම ලබන දරුවන් සඳහාද එකම ලිපිය නැවත වරක් ලියනු ලැබේ