Monday, June 7, 2021
මෙහිලා බල රුපසටහන නිවැරදිව අන්දගැනීම බොහොඕ දරුවනට මුහුණ පෑමට සිදුවූ පොදු කරුණකි. නමුදු දරුවනි ඔබ පළමුව ගැටලුව හොඳින් කියැවීම යෙහෙකි. කුහර ගෝලයකින් තනු අරය a වූ පාත්රය පිහිටවූ ආකාරය විස්තර කල තිබේ එය වටහාගැනීමට නොහැකිව දරුවන් එය පැටලුනු නූල් පන්දුවක් බවට පත්කරගෙන තිබුණි. පළමුව මෙහි ගැට්ටේ එක එක ලක්ෂයට අඳි අරය යනු පාත්රයෙහි අක්ෂයට ලම්භකව ගැටිය හරහා යන තලය අදහසවේ(සැකෙවින් ගත කල ගැටියේ තලය නොවේද ) ඉතින් මෙය සිරසට සාදන කෝණය ඇල්ෆා ලෙස දී ඇත .බොහෝ දරුවන්ට මෙම කෝණයේ මනිනලද ඇත උඩු සිරසද යටිසිරසාද වශයෙන් ගැටලුකාරී තත්ත්ව තිබෙනු දැක ඇත.මෙහිදී මෙවන් ගැටලුවක දෙනලද කෝණය නිතතිව සුළු කෝණයකි .එමනිසා එලෙස ලකුණු කිරීමට වගබලාගතයුතුය.A ලක්ෂය ඔස්සේ පවතින අරයද සිරසට බීට කෝණයක් ආනතව පවතින බව දී ඇතිමුත් A හි සාපේක්ෂ පිහිටුම ගැන ඒකතල බලසමතුලිතතාවය සම්බන්ධයෙන් වන ප්රමේයයන් හා සැසඳීම යෙහෙකි .A ලක්ෂය පාත්රයේ ගුරුත්ගැව කේන්ටිද්යේරයෙහි තලයේ පහල කෙලවර ගැටියේ තිරස්මට්ටමට ඉහලින් වූවානම් බලසමතුලිතතා නියම කිසවක් පිලි නොපදි (වෙනම බ්ලොග් පිටුවකින් ඒකතල බල පද්ධති හා එහි ජ්යාමිතිය අතර සම්බන්ධතාවය ගොඩනැගෙන අයුරු ක්රමානුරුපිව පෙළගැස්වීමට බලාපොරොත්තුවෙමි ).තවද A ගෝලයෙහි කේන්ද්රය හරහායන්නා වූ සිරස් රේඛාව පසු කරමින් පහල ගතියට ආසන්න ලක්ෂයක වුද බලසමතුලිතතා නියම පිළිනොපදි.බොහො ගණන් සමග ඔබ ප්රායෝගික පැතිකඩද මනාව හසුරමින් පරිනතවන කල මෙවැනි නොව මිට සංකීරණ රුඋපය වුද එකවර ගොඩනැගීමට අවශ්ය බුද්ධිය ගොඩනැගේ .ඒවෙනුවෙන් බොහොමයක් ගණන් තමන් විසින්ම විසඳීම යෙහෙකි .අභිලම්භ ප්රතික්රියා හ්හටගන්නා නීතියට අනුව ස්පර්ශ ලක්ෂ්යේදී පෘෂ්ටයට ලම්භක වන පරිදි A හිදී ප්රුෂ්ටය පාත්රය වේ .මෙලෙස හරස්කඩ පරාවල හෝ වෙනයම් හැඩයක් ඔබට ලැබුනානම් අභිලම්භ ප්රත්ක්රියාව කවර ආකාරයකට විඉජ සහ ජ්යාමිතිකව ගොඩනැගිය හැකිදැයි ඔබම තර්ක කරන්න (විෂය නිර්දේශයට අයත් නොවේ)නමුත් දන්දෙහි බැඳ ගැටියේ වැදුණු කල බොහෝ දරුවන් පුරුද්දට මෙන් දණ්ඩට ලම්භකව ප්රතික්රියාව ලකුණු කලද ඒ ගැන නිසි අවබෝධයක් නැත.අතිශය සියුම්ව සිතුවහොත් සාපේක්ෂව එම ස්ථානයෙහි පෘෂ්ඨය දන්දවේ.A හි අභිලම්භ ප්රතික්රියාව විෂ්කම්භය ඔස්සේ හා එය පරිධිය හමුවන ලක්ෂයේම අනෙක් අභිලම්භ ප්රතික්රියාව හමුවිය යුතුය .වෘත්තයක ජ්යාමිතියට අනුව එය තහවුරු කරගත හැක .D ලෙස දී ඇති ලක්ෂය දන්දෙ බර රේඛාව පරිධියත් A ඔස්සේ යන තිරස් රේඛාවේ චෙධනයත් වේ කොන නිවැරදිව සොයා ගනිමින් AD ආකාර දෙකකින් සමීකරණ ගොඩනැගීම අතිශය පහසු කරුණකි.එවිට යමෙකුට බලසමතුලිතතා නියම යෝදාඔගත්තේද යයි කුකුසක් ඇතිවිය හැක .අප බලරුපසටහන නිවැරදිව අන්දිමම බල සමතුලිතතා නියම භාවිතා කිරීමකි
Subscribe to:
Post Comments (Atom)
Introduction to R
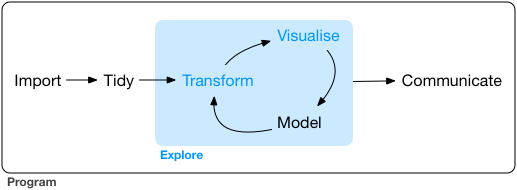
Introduction for R programming The goal of the first part of this book is to get you up to speed with the basic tools of data explorati...
-
My book is about to release. it may contain over 1000 questions. you can contact us to get more information
-
https://www.fiverr.com/s2/6a786172e6 https://www.fiverr.com/s2/6a786172e6
-
Introduction for R programming The goal of the first part of this book is to get you up to speed with the basic tools of data explorati...



No comments:
Post a Comment